Hatcher 0.6

Hatcher, Algebraic Topology, Chapter 0

6. (a) Let $X$ be the subspace of $\mathbb{R}^2$ consisting of the horizontal segment $[0,1]\times\{0\}$ together with the vertical segments $\{r\}\times[0,1-r]$ for $r$ a rational number in $[0,1]$ . Show that $X$ deformation retracts to any point in the segment $[0,1]\times\{0\}$ , but not to any other point (see the preceding problem).

(b) Let $Y$ be the subspace of $\mathbb{R}^2$ that is the union of an infinite number of copies of $X$ arranged as in the figure below. Show that $Y$ is contractible but does not deformation retract onto any point.

(c) Let $Z$ be the zigzag subspace of $Y$ homeomorphic to $\mathbb{R}$ indicated by the heavier line. Show that there is a deformation retraction in the weak sense (see Exercise 4) of $Y$ onto $Z$ , but no true deformation retraction.

Figure 1
The spaces mentioned above

Proof. (a) Let $X$ be the subspace of $\mathbb{R}^2$ shown on the far left of Figure 1 consisting of the horizontal segment $[0,1]\times\{0\}$ together with the vertical segments $\{r\}\times[0,1-r]$ for $r$ a rational number in $[0,1]$ . First, note that the segment $J=[0,1]\times\{0\}\cong[0,1]$ deformation retracts onto any point $x_0\in J$ by way of the straight-line homotopy $r_t$ which fixes $x_0$ for all $t\in I$ and which linearly “squeezes” the intervals $[0,x_0)$ and $(x_0,1]$ towards their right and left endpoints, respectively. Algebraically, then, $r_t$ is the family of maps for which

$[0,x_0)\mapsto [(1-t)x_0,x_0)$ and $(x_0,1]\mapsto (x_0,x_0+t(1-x_0)]$ .

Next, note that the space $X$ deformation retracts onto the space $J\cap\mathbb{Q}$ in a fashion similar to the one above, namely by way of the family of maps which, for each rational $r\in\mathbb{Q}$ , maps the segment $\{r\}\times[0,1-r]$ to the point $(r,0)$ continuously with respect to $t$ as $t$ ranges through $I=[0,1]$ . Denoting this family of maps $s_t$ , it follows that the space $X$ deformation retracts to any point $x_0\in J$ by way of the composition $\Gamma_t$ , where

$\Gamma_t = \left\{ \begin{array}{rl} r_{1-2t}, & 0\leq t\leq 1/2\\ s_{2t-1}, & 1/2\leq t\leq 1 \end{array} \right.$ .

Finally, the goal is to show that $X$ fails to deformation retract onto any point $x\in X$ not on the segment $J$ . For a contradiction, suppose that there does exist such an $x\in X\setminus J$ for which a deformation retraction $f_t:X\to\{x\}$ exists. By the result of Exercise 0.5, it follows that every neighborhood $U$ of $x$ in $X$ contains a neighborhood $V\subset U$ of $x$ for which the inclusion $\iota:V\hookrightarrow U$ is null-homotopic. Evidently this is bad; how come?²

Note that $X$ is path-connected¹ but that $X\setminus J$ clearly isn’t path-connected. In particular, suppose $U$ is a neighborhood of $x$ in $X\setminus J$ . Then $U$ can be thought of as an open ball in $\mathbb{R}^2$ , disjoint from $J$ , and intersecting a countably infinite number of line segments, all of which are disjoint. Thus, $U$ fails to be path-connected. For the same reason, any neighborhood $V\subset U$ containing $x$ must also be path-disconnected, whereby it follows that $V$ cannot contract to a point. Hence, $\iota:V\to U$ cannot be homotopic to the constant map, contradicting the result of 0.5.

(b) Let $Y$ be the subspace of $\mathbb{R}^2$ shown in the rightmost part of Figure 1 consisting of an infinite number of copies of $X$ arranged as above. The fact that $Y$ fails to deformation retract onto any point is an almost-identical application of Exercise 0.5 to the one mentioned in (a). In particular, given a point $y\in Y$ , there exists neighborhood $U$ of $y$ in $Y$ that is necessarily path-disconnected. This claim follows immediately from (a) if $y$ fails to lie on the zigzag subspace $Z\subset Y$ (see part (c)). In the case that $y\in Z$ , this can be heuristically described in cases as follows.

Suppose $y\in Z$ fails to be one of the “vertex points”. Any neighborhood $U\ni y$ in $Y$ intersects two “fundamentally different” countably infinite disjoint collections of line segments of $Y$ , one collection which is directed “bottom-left-to-top-right” – call it $C_1$ – and one which is directed “top-left-to-bottom-right” – call it $C_2$ . In this case, any point on a segment in $C_1$ cannot be connected to any point in $C_2$ because of the fact that $Z$ intersects only one of $C_i$ , $i=1,2$ .

The argument for $y$ a “vertex point” of $Z$ is similar with the exception that an open neighborhood $U$ of $y$ now intersects three fundamentally different collections of line segments, two of which – say $D_1$ and $D_2$ – are directed in a parallel fashion (either “bottom-left-to-top-right” or “top-left-to-bottom-right”) with the third, $D_3$ , directed in the other fashion. In this case, any point in $D_i$ , $i=1,2$ , can be connected to any point in $D_3$ by a path due to the fact that $Z$ intersects $D_3$ and one of $D_i$ , $i=1,2$ . On the other hand, $Z$ intersections precisely one of $D_1$ or $D_2$ , meaning that no path in $Y$ exists connecting points in $D_1$ to $D_2$ .

Now, it suffices to show that $Y$ is contractible. Note, first, that $Z\cong\mathbb{R}$ is clearly contractible. Next, note that the space $Y$ can be retracted (not deformation retracted) onto $Z$ by way of a modified version of the family $r_t$ given in part (a). More precisely, the map $r:Y\to Z$ is a retraction, where $r$ is the constant map on $Z$ and where $r$ maps any “straw” $\{r\}_i\times[0,1-r]_i$ onto the point $(0,r)_i\in Z_i$ , where the subscript $_i$ here denotes the elements in the $i^\text{th}$ copy of $X$ .³ Therefore, it’s been shown that $Y$ retracts onto the zigzag $Z$ which is a contractible subspace, thereby proving that $Y$ itself is contractible.

(c) To begin, note that there is clearly no (strong) deformation retract of $Y$ onto $Z$ , else the composition with the deformation retraction of $Z\cong\mathbb{R}$ to a point as noted in (b) would yield a deformation retraction of $Y$ to a point. This contradicts the result of (b). As such, it’s enough to show that the “contraction” of $Y$ onto the zigzag subspace $Z\subset Y$ is a (weak) deformation retraction. To that end, let $s_t$ be the family which fixes the space $Z$ and takes each “leaf” $\{r\}_i\times[0,1-r]_i$ and shrinks its length by a factor of $t$ , i.e.

$s_t:\{r\}_i\times[0,1-r]_i\mapsto \{r\}_i\times[0,t(1-r)]_i$ for all $t\in I,i\in\mathbb{Z}$ (see [3]).

Continuity here is immediate, and because the three conditions outlined in Exercise 0.4 for weak deformation retractions are clearly met, the result follows. $\square$

1. The path-connectedness of $X$ is easily shown by an analysis of cases for arbitrary points $x\neq y\in X$ . If $x,y\in J$ , the result is immediate. If one of the pair is in $J$ and the other isn’t (WLOG, $x\in J$ and $y\in\{r\}\times[0,1-r]$ ), then the path $y\mapsto (r,0)\mapsto x$ works. Finally, if $x\in\{r_1\}\times[0,1-r_1]$ and $y\in\{r_2\}\times[0,1-r_2]$ , then the path $y\mapsto (r_2,0)\mapsto(r_1,0)\mapsto x$ works as well.

2. Ideas for the final part of this proof were borrowed from the document found here: http://www.math.uchicago.edu/~may/263/ps1.pdf.

3. Here, we’re identifying $Y$ with the union $\cup_{i\in\mathbb{Z}}X_i$ where $X_i=X$ for all $i\in\mathbb{Z}$ . In particular, the $_i$ notation is a sloppy, lazy way of designating which copy $X_i$ of $X$ we’re considering.

11 thoughts on “Hatcher 0.6”

Gary

September 16, 2013 at 5:54 pm

Your map in (b) isn’t continuous, as it keeps the points in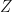 $Z$ fixed and moves the straws. In fact, if it were continuous, it would be a deformation retraction in the strong sense, and we know this is not possible.

- castover
  
  October 3, 2013 at 4:47 pm
  
  Hmmmmm. I seem to have overlooked something when I was attempting to understand what needed to happen in this problem originally. That now seems silly.
  
  Would you perhaps be willing to shed some insight on a “not broken” way to proceed with this part of the problem?
  
  I appreciate both your oversight and your insight.
  
  - B
    
    September 27, 2015 at 8:44 pm
    
    Hi, did you ever figure out this issue in part b)? I am having trouble coming up with a continuous homotopy as well.
  - castover
    
    September 28, 2015 at 4:29 am
    
    I honestly didn’t even think about it after the other comment which pointed out my dumbness. If I had to think about it (which I don’t really want to do but will for 2 seconds because you asked so nicely ^_^), I’d say that because the previous comment indicates badness in the fact that the points in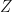 $Z$ are kept fixed while the straws are moved, perhaps a solution would be shrink 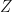$Z$ at the same time the straws are being shrunk? Imagine unfolding the zig-zag space into a copy of $\mathbb{R}$ with “straws” periodically placed in alternating fashion (some pointing upward, some facing downward), and imagine using the same time parameter to retract the $\mathbb{R}$ part and the straws onto the $\mathbb{R}$ part? Not sure; try this, and if it works, please do comment with any/all details!
Hoang

March 6, 2014 at 11:15 pm

in last statement part b) you said that Y retracts on to a zig-zag Z that is contractible then it implies Y is contractible. This is not true in general and it is not clear in this content. It is good idea if you prove (c) first and use previous exercise ( i.e exercise 4) to show Y is homotopy equivalent to Z, it follows that Y is homotopy equivalent to a point.

- kimgy777
  
  May 6, 2017 at 10:49 am
  
  If Y retracts on to a zig-zag Z that is contractible then it implies there is a continuous function F(deformation retract) from Y * I to into Y such that F(y,0)=y, F(Y,1)=Z for all y in Y.
  And since Z is contractible, there is a continuous function H (contraction) from Z*I to Z.
  Then for each y in Y, we can construct path product alpha_y by two functions F and H.
  If we define new function K:Y*I -> Y such that K(y,t)=alpha_y (t) , then it will be continuous and a contraction of Y
  
  - Newt
    
    August 15, 2017 at 2:02 am
    
    Retractions and deformation retractions are not the same thing. A retraction is simply a continuous map from a space into a subspace that is the identity when restricted to that subspace. Every space retracts to a single point set (by the constant map). By this logic, every space is contractible.
DB

February 5, 2017 at 9:53 pm

It seems to me that in the fourth paragraph seventh line of part b that the solution should read (r,0) instead of (0,r) because we want the height of the straws to become 0.

Yunan

November 6, 2020 at 4:51 pm

In part(a), the second half, I can not understand why V is necessarily dis-path-connected. I know U consists of line segments, but V subsets to U. Why not V be the one line containing x?

- Yunan
  
  November 6, 2020 at 5:07 pm
  
  Resolved. Thank you so much!
  
José Luis Ortiz

March 17, 2021 at 6:00 pm

I think a solution for b is: F(x,t) = f_x(t) a path connecting x with a in Z(it’s not necesarry this last assumption. I believe). For c, F(x,t) = h_x(sqrt(2)t) a function that moves sqrt(2) units to the right to the point x. As you can see continuity is not spoil in this way.