Today was grocery day in the Stover household, which means we basically spent the day driving around, picking up amazing savings due to my wife’s couponing and essentially getting nothing else done whatsoever.
Fortunately, I was able to squeeze in about 30 minutes of math while sitting in the local Target’s snack bar / Starbucks area. In particular, I took some time to read a bit further into my professor’s paper on M-conformal Cliffordian functions, and in so doing, I came to a realization.
The last time I wrote here about that paper, I sketched a small proof of an elementary claim that probably required no proof. As a result of that entry, today has been as complete roller coaster for me.
First, I thought I’d misquoted the definition of a function  being monogenic: My original claim was that
being monogenic: My original claim was that  for monogenic functions, but today, I miscalculated the partials for an example that led me to believe that
for monogenic functions, but today, I miscalculated the partials for an example that led me to believe that  was actually the criteria. That’s not correct at all.
was actually the criteria. That’s not correct at all.
Now, I realize what the criteria really is, but at the same time I realize that one small detail of that proof was incorrect. In particular, I combined the summed expressions for 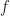 and
and  , respectively, to be a single sum ranging from
, respectively, to be a single sum ranging from  instead of a term for
instead of a term for  and
and  , respectively, plus a sum for
, respectively, plus a sum for  . Later, when there were two parameters
. Later, when there were two parameters  in the sum, I claimed that
in the sum, I claimed that  implies that
implies that  ; this, of course, is false, since
; this, of course, is false, since  is identified with 1 so that
is identified with 1 so that  . On the other hand, with a proper bit of rigor, the proof is still essentially correct.
. On the other hand, with a proper bit of rigor, the proof is still essentially correct.
Here’s why:
Here’s one way to think about the problem. Let  , an equivalent representation of which is
, an equivalent representation of which is  where
where  and where
and where  represent the scalar and vector parts of
represent the scalar and vector parts of 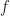 , respectively. In particular, then, if we consider
, respectively. In particular, then, if we consider  to be the derivative of
to be the derivative of 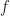 , it follows that
, it follows that  precisely when
precisely when ![D_n[\mathbf{sc}(f)]=0](https://s0.wp.com/latex.php?latex=D_n%5B%5Cmathbf%7Bsc%7D%28f%29%5D%3D0&bg=ffffff&fg=111111&s=0&c=20201002) and
and ![D_n[\mathbf{vec}(f)]=0](https://s0.wp.com/latex.php?latex=D_n%5B%5Cmathbf%7Bvec%7D%28f%29%5D%3D0&bg=ffffff&fg=111111&s=0&c=20201002) . With regards to the scalar part of
. With regards to the scalar part of 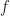 , this implies that
, this implies that
 .
.
In particular, then, the vector  , and so each component must be zero. Hence,
, and so each component must be zero. Hence,  for
for  .
.
If we then turn our attention to the vector part of 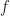 , we see that
, we see that ![D_n[\mathbf{vec}(f)]=0](https://s0.wp.com/latex.php?latex=D_n%5B%5Cmathbf%7Bvec%7D%28f%29%5D%3D0&bg=ffffff&fg=111111&s=0&c=20201002) , i.e. that
, i.e. that
![\begin{array}{rcl}0 & = & \displaystyle\left(\frac{\partial}{\partial x_0}+\sum_{l=1}^n e_l\frac{\partial}{\partial x_l} \right)\circ\left(\sum_{k=1}^n u_k(x)e_k\right) \\[2em] & = & \displaystyle\sum_{k=1}^n \frac{\partial u_k}{\partial x_0}e_k + \sum_{k,l=1}^n e_l\,e_k\frac{\partial u_k}{\partial x_l}\,\,\,\,\,\,\,\,\,\,(1)\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D0+%26+%3D+%26+%5Cdisplaystyle%5Cleft%28%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x_0%7D%2B%5Csum_%7Bl%3D1%7D%5En+e_l%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial+x_l%7D+%5Cright%29%5Ccirc%5Cleft%28%5Csum_%7Bk%3D1%7D%5En+u_k%28x%29e_k%5Cright%29+%5C%5C%5B2em%5D+%26+%3D+%26+%5Cdisplaystyle%5Csum_%7Bk%3D1%7D%5En+%5Cfrac%7B%5Cpartial+u_k%7D%7B%5Cpartial+x_0%7De_k+%2B+%5Csum_%7Bk%2Cl%3D1%7D%5En+e_l%5C%2Ce_k%5Cfrac%7B%5Cpartial+u_k%7D%7B%5Cpartial+x_l%7D%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%5C%2C%281%29%5Cend%7Barray%7D&bg=ffffff&fg=111111&s=0&c=20201002) .
.
Note that the two sums in  sum to zero precisely when each sum itself is equal to zero due to the linear independence of the basis elements
sum to zero precisely when each sum itself is equal to zero due to the linear independence of the basis elements  ,
,  . In particular, then, the second sum in
. In particular, then, the second sum in  equals zero and is precisely the sum I used for the matrix analogy in my original solution. Among the necessary corrections is to note that the matrices
equals zero and is precisely the sum I used for the matrix analogy in my original solution. Among the necessary corrections is to note that the matrices  cited there should be
cited there should be  matrices instead of
matrices instead of  . Recall also that the first equation in the system of equations shown in the original entry – the equation
. Recall also that the first equation in the system of equations shown in the original entry – the equation  – is achieved by combining the equation of “mixed partials” of the form
– is achieved by combining the equation of “mixed partials” of the form  from the second sum in
from the second sum in  with the fact that
with the fact that  from above.
from above.
whew
This, sirs and madames, is what happens when one doesn’t protect against carelessness. I need to weed that out of my repertoire and fast. Blah.
Anyway, I’m gonna try to learn some Algebraic Geometry and maybe apply that to some 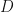 -module theory. Until next time….
-module theory. Until next time….
of complex polynomials in
and later as a “variety that can be embedded in affine space as a Zariski-closed set” (Smith et. al., An Invitation to Algebraic Variety). Then, half a book later or more (it’s on page 144 of the aforementioned book), it’s said that an (abstract) algebraic variety is a topological space with an open cover consisting of sets homeomorphic to affine algebraic varieties which are glued together by so-called transition functions that are morphisms in the category of affine algebraic varieties.
-modules.
