Reading, and reading, and teaching, and reading, and reading, and…

So, to summarize the direction of my most recent mathematical endeavors: I woke up and decided that part of my aspiration was to become a geometric topologist, and I did that despite the fact that topology is (far and away) my worst subject.

That sounds precisely as terrible as it probably is.

The long, hard road to updates

So since coming back around here last week, I’ve been working on an update.

Of course, I’d be lying if I said I’d been working non-stop on an update, but I have, in fact, been working on one. I’d say I’m a solid 75% finished with it now, even though it’s (a) not going as quickly as I’d expected and (b) probably not going to be written the way I’d anticipated. Oh well; such is life, I guess.

I’m down to my last seven days of Wolfram employment, and to say I’m a sad robot is understatement of the year. I’m hoping the hustle and bustle of a new school term with new responsibilities and opportunities and excitements will curb that somewhat, but at this point, I’m not 100% convinced.

Among new things that have happened in the last week:

• FSU made office assignments for the new year. Apparently I’m staying put. As much as I’d have liked a new office (you know, since my CEILING COLLAPSED AND DESTROYED ALMOST EVERYTHING I HAD THERE(!!!)), I don’t like the hassle that comes with doing something new. I’ll already be doing enough new things; figuring out a new office situation isn’t something I want to add to that list.
• Fall schedules have been entered. I’m officially taking the third semesters of abstract algbera (field theory + categories, I think) and topology (advanced algebraic topology), as well as a course on complex manifolds (taught from an algebraic geometry perspective, I’d guess) and Riemannian manifolds. I’m excited. Sincerely.
• I’ve gotten my change of residency file 95% compiled. Monday will be the day to finish it off and submit it.
• I’ve finally started training for my new gig with Pearson. I’m less than thrilled with the progress so far. We’ll see.

Otherwise, things have been kinda the same: I’ve been doing a lot of Wolfram stuff, I’ve been taking more time away to hang with my family, and I’ve been somehow managing to not think about the nervousness I’ll invariably feel when new TA responsibilities, etc., pick up.

Things are good, I’d say, even though I’ve got a lot of things I need to start doing otherwise. I need to start reading the books potential advisers have suggested; I need to start doing more independent research; I need to start getting back in school mode.

For the first time in a really really long time, I’m enjoying being in not-school mode. I wonder if this is that changing tide I always heard so much about.

Anyway, expect a new content entry soon enough. And maybe some to follow that one. We’ll see.

Peace.

Back again

So, I knew it had been a while since I’d been around here, and even longer since I’ve posted anything of substance. Little did I know, however, that it had been almost a month since I’d been around and almost two months since coming here and posting anything even remotely of substance.

That’s definitely not how I envisioned this blog thing going.

Here’s a small list of what I’ve been up to:

• I snagged that gnarly internship at Wolfram that I posted about back in the day. It saddens me to say that today is the beginning of week seven there; the contract I signed was for eight weeks which, as I’m sure you can deduce, means that my time is almost up. Never in my life have I done something that’s made me enjoy working as much as this internship has. I’ve loved every single second of it and just thinking about it ending makes me tear up a bit.
• I took a summer class in foundations of math. That class has already come and gone. We covered nonstandard analysis, basic set theory, cardinals, ordinals, and a bit of other stuff throughout, and despite the fact that the overall course wasn’t the most well-oiled, beneficial thing I’ve ever experienced, it was enjoyable overall. The workload was intense, though – like, seriously, intense – and there were weeks that that class + my TA duties + my Wolfram internship had me logging 120 hours of work. I’d be lying if I said I don’t enjoy hard work, though, and in this instance, it paid off: I managed to secure an A in this course and bring my overall graduate GPA up to 3.71. That’s a victory I’ll take.
• I applied and got passed over for a really gnarly graduate fellowship offered by my department. I was really excited leading up to it and was really really down afterwards. I haven’t thought about it since, though, so I guess that means it wasn’t too detrimental to my existence.
• I’ve been in frequent conversation with one of the professors in my department who I most admire and he’s helped me schedule a study-plan to better myself for the potential of working with him / working in his area. He does work in Geometric Topology but has expertise that spans lots of other areas, too, including dynamical systems, chaos, and geometric group theory. I’m hoping to have an adviser picked by the end of fall and as of now, he’s in my top-3. Working with him would be an honor, and that is in no way and overstatement.

There are many things missing from that list that sadden me a bit. For one, I got to spend very little time with my family over the break. I also got to spend very little time maintaining the independent studies I’d lain out and begun earlier in the summer. School starts back in just a couple weeks and one of the things I’m most glad about is being able to spend a little more time working towards that goal. I’m also pretty excited about my classes this semester, and about getting more acquainted with professors in the department so as to narrow down my list of potential advisers.

I’m excited about my career right now. That’s always a good thing.

I’m going to try to get myself back into the swing of updating here. Perhaps that’s something I can work on tomorrow, say, but there’re no promises.

Good night, WordPress. I hope this is delivered to peaceful eyes and rested minds.

Peace.

Revisiting, and something light

Well, today was the fourth day of my official employment with Wolfram. This job is absolutely amazing; I couldn’t be more stoked. It’s saddening, of course, that I’m not spending my days engulfed in the books I’d been looking at earlier in the summer; it’s also a bit saddening that I have less time to spend with you beautiful people. Regardless, things are pretty amazing and overall, I couldn’t be happier.

I wanted to take some time to swing by here and say something, though, and fortunately for me, my TA duties this semester have yielded me something of precisely the right balance of depth (or lack thereof) and length (or brevity) to be fitting for tonight’s (this morning’s) pit stop.

On Wednesday (July 3), I was sitting in a precalculus class, doing Wolfram stuff and vaguely listening to what the instructor was talking about at the time. The topic? Logarithms. As someone who’s solo-taught precalculus before, I know precisely how little students understand – or like – or care – about logarithms. I also know how much we try to convince them to believe without their understanding which – among others – has to be a primary cause for their confusion and disdain.

One thing we try to get them to believe? The change of base formula. The change of base formula says that given a base 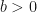, , 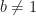the quantity 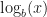is equal to the quantity

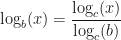where , .

This information is shared with students at that level largely so they can feel comfortable evaluating an expression like in their calculators given only the capacity to utilize and functionality. Surely, they never really need to know it.

And then I realized…

In all my years in mathematics, I’ve never actually seen this rule proven before. That, of course, sparked my interest, and so I went back to my office and jotted the (surprisingly simple) proof on my whiteboard just to appease my curiosity. Here’s the way that goes:

Proof of The Change of Base Formula.
Let 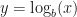so that . In particular, then, it follows that for , ,

.

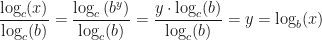I think I may force my next round of precalculus students to know that. It keeps ’em fresh, on their toes, where they gotta baayayaeeee….

Did anyone just catch my reference to ‘Heat’? Or, rather, my reference to Aries Spears’ reference to ‘Heat’?

I hope everyone’s 4th was safe and that there were only minimal injuries due to inebriation, explosives, and general tomfoolery.

Until next time….

Hump Day Math Day

Well, it’s Wednesday.

Generally, Wednesday is the cause for much joy because it means the terrible Mondays and Tuesdays are things of the past and that the future – those Fridays and Saturdays – are right around the corner. It makes sense, then, that Wednesdays would be good work days too: It should intuitively mean that the drag-assery of Mondays and Tuesdays has subsided and that the “time flies when you’re having fun” of Fridays and Saturdays has caught hold.

That hasn’t been the case here on the math front, today.

I’ve spent the better part of the morning and afternoon battling a migraine, which means I’ve held out on the “read new books” front (so long, Kobayashi and Nomizu…) and have instead been leisurely contemplating some of the unfinished problems from algebraic topology (…and hellllllllllo, Dr. Hatcher!). I’ve made some progress (read: I’ve done two problems), but it’s definitely not something to write home about.

But hey: Some days you’re the dog and some days you’re the hydrant.

I’ve finally reached the cluster of Hatcher problems dealing with CW complexes, and because I’m so genuinely awful at them, I’m going to take some time to read around and try to get a better grasp before moving forward. I have a good general idea and I can usually do some problems / work with the things themselves, but I always have a hard time processing the technical details thereof. Something about that whole connecting cells to cells by way of continuous maps that do some stuff on the boundary and yadda yadda yadda just never has settled with my brain cells.

And that, friends, is the point of summer: To force unsettled things to settle.