S^3 (the most basic prime manifold) is prime

So a while ago, I was reading Hatcher’s notes on 3-manifolds. In there, he defines what it means for a manifold to be prime and states, casually, that the 3-sphere is prime. He later says that it follows immediately from Alexander’s Theorem as, and I quote: Every 2-sphere in bounds a 3-ball. And that’s it. Done.

Wait, what?!

Elsewhere, Hatcher expands his above statement: …every 2-sphere in bounds a ball on each side…[and h]ence is prime. Again, though, it isn’t accompanied by anything, and while this is clearly a trivial result, I just couldn’t see it for the longest time…I knew that it followed from a number of things, e.g. the fact that is the identity of the connected sum operation, that is irreducible (and that every irreducible manifold is prime), that one gets the trivial sum by splitting along a 2-sphere in which bounds a 3-ball in , etc. Even so, I didn’t want to leverage some enormous machinery to deduce the smallest of results and what I really wanted was for someone to tell me what I was missing. So I never stopped thinking about this, even after moving forward, until finally – it just clicked!

I figure other people who are as visualization-impaired as I may benefit from seeing this explained in greater depth, so in lieu of typing a blog post containing something new and attention-worthy, I figure I’d share this instead. Details after the break.

Week 3, Day 1 or Properties of Lie Brackets

Today is the first day of the third week of the semester. I know that counting down like this is going to make it seem longer than it already seems, but it seems so long that I can’t seem to help remaining conscious of the precise time frame I’m dealing with.

Such is life, I suppose.

I’ve noticed an amusing trend in my page views involving solutions from Dr. Hatcher’s book, namely that I’ve been receiving an abnormally-high level of page views lately, almost all of which seem to center on those solutions. I guess that means that the semester has started elsewhere too and that people find topology as difficult and frustrating as I do.

For those of you who fit this bill and who are reading this right now: My plan is to start doing more problems ASAP, so that page might get its first update in quite a while.

Today, though, I want (read: need) to talk about differential geometry. In particular, we spent some time in class last week discussing the Lie bracket and its properties, and because we have a derivation of one particular property, I wanted to take the time to put that here for my own benefit.

Half-June

So today wasn’t really my day, overall. Generally speaking, I woke up feeling congested and nasty, I spent the whole day with a migraine, and I was only not-lethargic for about four hours total overall.

Unsurprisingly, then, I realllly couldn’t force my brain to do any real math. For that reason, I completely avoided reading new things and instead typed up the expository analysis entry during the middle part of the afternoon. I ended the night doing some solutions for Hatcher – Chapter 0 of which I’m hoping to knock out soon to begin Chapter 1 – and drawing (really really) poor diagrams in MSPaint. I’ve emailed Dr. Sjamaar from Cornell to ask how he gets his diagrams drawn, but thus far have heard nothing back.

Pleeeeeeease don’t leave me hangin’, Dr. Sjamaar: My blog is evidence that I’m in desperate need of your resource knowledge!

Anyway, it’s almost 2am and I’m about to call it a night.

Auf Wiedersehen.

Paradoxes, paradoxically

So I was able – fortunately – to wake up early and to do some legit reading, despite having only a handful of sleep hours (4-ish?). That’s a definite positive. Right now, I’m about 30 minutes away from a forced obligation (that’s a definite negative), but I wanted to use the 30 minutes I have to still do something constructive. Rather than spend this time wracking my brain with really difficult, hard-to-understand reading that would leave me mentally exhausted for the aforementioned obligation, I decided to come here and write a little exposition regarding something mathematical.

In particular, I’m going to talk about the so-called Richard’s Paradox (see here).

Of course, the fact that I’m avoiding theoretical math to postpone mental exhaustion while using the time to come here and talk about theoretical math is a bit of a paradox as well, so I’ll basically be expositing, paradoxically, about paradoxes.

You have no idea how much I crack myself up.

The ideology that birthed Richard’s paradox is intimately tied to the idea of metamathematics, that is, the study of metatheories – theories about mathematical theories – using mathematical ideas and quantification. I’m not going to get too deeply involved in the discussion on that particular topic; the interested reader, of course, can scope out more here.

To begin, we let 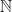denote the set of nonzero positive integers (aka, the natural numbers) and we investigate the collection of all “formal English language statements of finite length” which define a number 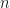of 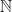. For example, The first prime number, The smallest perfect number, and The cube of the first odd number larger than five are such statements, as they verbally describe the numbers 2, 6, and 7³=343, respectively. On the other hand, statements like The number larger than all other numbers and Scotland is a place I’d like to visit fail to make the list due to the fact that the first doesn’t describe a number in 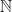and the second doesn’t describe a number at all. Let 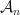denote the collection of all so-called qualifying statements, that is, statements that do describe elements .

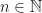Note, first, that the collection 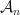is infinite due to the fact that the statements The i^th natural number is a qualifying statement for all . It’s also countable: Only a countable number of words exist in the English language, and each statement in 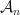consists of a finite union of these countably many words. This fact, along with obvious language considerations, says that 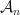can actually be given an ordering.

Indeed, consider a two-part ordering: First, organize the statements in 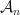by length so that the shortest statements appear first, and then organize statements of the same length by standard lexicographical (dictionary) ordering. The result is an ordered version of the countably infinite collection 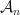which we’ll again denote by .

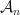As of now, almost nothing has been done.