Yesterday, Today, and Forever

Yesterday was a day filled with reading.

Also, by and large, yesterday was a day consisting entirely of (differential) geometry / topology, so it’s really no surprise that – again – my dreams were all math related and tied to that general realm of theory. More precisely, I spent my entire sleep cycle pondering the Poincaré Conjecture (can we call it the Perelman Theorem yet?) and Ricci Flows. That’s certainly a night well spent.

Unsurprisingly, my day today will be largely similar. I downloaded a bunch of resources concerning the aforementioned topics (Poincaré-Perelman and Ricci Flows), as well as some (more) texts on Riemanninan Geometry (which I started perusing yesterday). Also in the works: A colleague of mine (who I’ll call DW2) and I have decided to work through Atiyah and MacDonald’s Introduction to Commutative Algebra, and I’m pretty sure if I don’t spend a significantly-larger amount of time on my professor’s Clifford paper, I’m going to have zero things about which to ever talk with him…

…then there’s the algebraic geometry stuff I’m working on in Eisenbud and Harris / Dummit and Foote, and the material from the seven or so other books I’m reading through concurrently right now….

Every day I’m huss-uh-lin’….

I have some things I want to write here later – expository things and what not – but for now, it’s just this check-in. Auf Wiedersehen!

Paradoxes, paradoxically

So I was able – fortunately – to wake up early and to do some legit reading, despite having only a handful of sleep hours (4-ish?). That’s a definite positive. Right now, I’m about 30 minutes away from a forced obligation (that’s a definite negative), but I wanted to use the 30 minutes I have to still do something constructive. Rather than spend this time wracking my brain with really difficult, hard-to-understand reading that would leave me mentally exhausted for the aforementioned obligation, I decided to come here and write a little exposition regarding something mathematical.

In particular, I’m going to talk about the so-called Richard’s Paradox (see here).

Of course, the fact that I’m avoiding theoretical math to postpone mental exhaustion while using the time to come here and talk about theoretical math is a bit of a paradox as well, so I’ll basically be expositing, paradoxically, about paradoxes.

You have no idea how much I crack myself up.

The ideology that birthed Richard’s paradox is intimately tied to the idea of metamathematics, that is, the study of metatheories – theories about mathematical theories – using mathematical ideas and quantification. I’m not going to get too deeply involved in the discussion on that particular topic; the interested reader, of course, can scope out more here.

To begin, we let 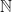denote the set of nonzero positive integers (aka, the natural numbers) and we investigate the collection of all “formal English language statements of finite length” which define a number 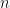of 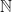. For example, The first prime number, The smallest perfect number, and The cube of the first odd number larger than five are such statements, as they verbally describe the numbers 2, 6, and 7³=343, respectively. On the other hand, statements like The number larger than all other numbers and Scotland is a place I’d like to visit fail to make the list due to the fact that the first doesn’t describe a number in 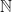and the second doesn’t describe a number at all. Let 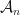denote the collection of all so-called qualifying statements, that is, statements that do describe elements .

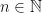Note, first, that the collection 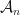is infinite due to the fact that the statements The i^th natural number is a qualifying statement for all . It’s also countable: Only a countable number of words exist in the English language, and each statement in 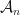consists of a finite union of these countably many words. This fact, along with obvious language considerations, says that 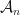can actually be given an ordering.

Indeed, consider a two-part ordering: First, organize the statements in 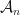by length so that the shortest statements appear first, and then organize statements of the same length by standard lexicographical (dictionary) ordering. The result is an ordered version of the countably infinite collection 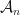which we’ll again denote by .

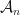As of now, almost nothing has been done.

Idolatry, or The mathematician I wish I was

So as per my last post, I haven’t been around these parts much in the last couple days. I’ve been reading through a professor’s paper on Clifford Analysis and trying to bridge the gaps in understanding there; I also took some time to schedule an in-office meeting with another professor to discuss his research.

I’m always doing math, even if no math is getting done.

At some point in that time, I started digging around WordPress and looking specifically for math blogs and believe me when I tell you that a single discovery completely boosted my spirits.

Okay, in all honesty, it made me beam like a nerdy fangirl at Comic-Con.

Terence Tao has a WordPress.

Let me give you a brief rundown of why that’s significant for me:

Terence Tao is without a doubt near the top of my list of mathematical idols. This guy is amazing: The breadth of his work and the depth of expertise he’s been able to accrue in such a wide variety of topics is absolutely staggering. His publication list reads more powerful than the voice of god delivering commandments to Moses on Mount Sinai and the number of significant results he’s proven is staggering on any metric.

I’m never sure whether this sort of idolatry percolates up through the ranks of big-time, legitimate mathematicians. For example, I have a hard time imagining that Grigori Perelman spent days surfing the internet and pining over the abilities of mathematicians “better than himself,” mostly because I have a hard time imagining guys like that feeling inferior to anyone in terms of mathematical ability. Also, by and large, the number of my peers who seem to understand my thoughts when I gush over how amazing it would be to take a class at Cornell with Allen Hatcher or at MIT with Victor Guillemin, so to be honest, I’m not really sure what demographic of mathematician is incline to fangirl-ism or what about me forces me into that group. But I’ve digressed:

Long story short: Terence Tao is, to me, the standard by which we measure mathematicians. He’s the mathematician that I wish I could be, and to go one step farther, if I’ve accomplished 1% of what he has by the time I’m a crazy old mathematical recluse living in a shack in the mountains and yelling curses at various named-theorems, I’ll be a much larger success than I can presently imagine myself becoming…

…and he has a WordPress….

So suffice it to say, my Reader will be getting much more use now that I know this.

Also, among things to be getting more use: Things needed to do math. I’ve been slacking a bit lately, sleeping in and casually reading, but today’s the day I’m gonna take the plunge and go back to working arduously.

Today’s the day.

Happy Sunday, folks.