doctoral program

Posted by

0

Last week was the first of the big 3-manifolds events at IAS and overall, it was spectacular. The highlight, without a doubt, was Dave Gabai being amazing during the last talk of the week, but there were some other great moments too…

…and some not-so-great ones, including some woman whom I don’t know interrupting Genevieve Walsh‘s talk no fewer than 10 times to say random rude things about how it was not-good (which was untrue), unoriginal (only true in the sense that Dr. Walsh spent some time talking about general background that she didn’t claim to have invented), and a waste of time. I was pretty blown away that such things happened at pure math talks, but I guess pure math people are people too and – at the end of the day – people just look for a way to disappoint and/or bring down other people. :\

I learned a lot, though, and I came away with a new direction for my own research, so that’s going to be the goal moving forward: To balance the somewhat-regular yearly 3-manifolds talks at IAS with the stuff I need to figure out to get my own stuff knocked out.

Oh, and plus side: I actually got a full week of salaried work done! YAY FOOD! But the downside is that I’m having to drop $2k on random car things (making our tires able to withstand rain and snow and making it so that our heat keeps hypothermia at bay), so…YAY CREDIT CARD DEBT! ::wink::

Alright, well I’m awake for some dumb reason so I guess I’ll…try to do something…constructive. Or something. Hah.

Later, guys.

Algebraic Topology Notes

Posted by

0

Algebraic Topology Notes

A colleague of mine just shared these with me. This seems to have a more general introduction (i.e., an introduction with less assumed knowledge) than does Dr. Hatcher’s book. 

Study Plan + Hatcher Section 0 solutions

Posted by

0

So going into the summer, I had a pretty concise game plan of how I wanted things to work. I wanted (a) to exempt all my qualifying exams so that I’d have fewer have to’s on my agenda, and (b) to spend all the time I’d save through completing (a) split between (i) studies to help me with my required coursework next semester and (ii) studies to help me towards being able to research things I want to research.

Worst case scenario, of course, was that I didn’t exempt qualifying exams and had to incorporate preparation for those into the mix. As it stood, though, I had a clear idea of what my summer was going to consist of, academia-wise. I planned on taking the first week (i.e., last week) to casually do some independent research without a rigid schedule in place, which would turn into a regimented plan – beginning today and lasting until the beginning of fall – consisting of one hour of studying per day in each of the following fields:

  • Clifford Analysis.
  • Differential Topology/Geometry.
  • Algebraic Topology.
  • Abstract Algebra.

Among the four fields listed above, the first two were for me and me alone, whereas the last two were to help me for next semester.

It’s now 4:30am Tuesday. I didn’t spend Monday adhering to that regimen and, for all intents and purposes, I probably won’t today. There’s a long list of excuses I could give about how I had to go to the ER, about how my infant son is teething and angry, etc. etc., but the story is simply this: I made a regimen that I don’t seem to be able to stick to. Bing, bang, boom.

I’m going to do my best to get something constructive out of this summer, but I’m facing the sad reality that it probably won’t be what I’d planned. Boo hoo.

To aid my attempts, I’m going to try to put some of my solutions here as a way of forcing myself to stay dedicated. Somewhat. For now, here are some solutions for the Chapter 0 material from Hatcher.

Hatcher, Algebraic Topology, Chapter 0
1. Construct an explicit deformation retraction of the torus with one point deleted
onto a graph consisting of two circles intersecting in a point, namely, longitude and
meridian circles of the torus.

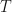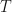Proof. Let T be the torus and let X=T\setminus\{\text{pt}\} be the space in question. By considering the square gluing diagram of the torus T sans a point, a diagrammatic representation for 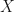X can be given as shown in Figure 1 below.

Hatcher 0.1
Figure 1

Note that the gray part of Figure 1 represents the fact that the torus 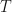T is filled in and that one can visualize the deformation retract in question by grabbing hold of the hole in 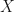X and stretching it out so that the diagram in Figure 1 is hollow (i.e., not filled in, i.e. all white, etc.). Thus, the deformation retract in question amounts to the projection of the interior of a square (the square representing the gluing diagram of 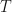T) onto its boundary, the formula for which can be attained by presupposing that the gluing diagram for 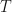T is placed in 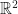\mathbb{R}^2 as J\times J where J=[-1,1]. Basic arithmetic shows that, for t\in I, the family f_t:I\times I\to\mathbb{R}^2 given by

f_t(x,y)=(1-t)(x,y)+t\left(\dfrac{(x,y)}{\max\{|x|,|y|\}}\right)

“does the trick.” Indeed, note that f_0(x,y)=(x,y), that f_1(x,y)=(x,y)/\max\{|x|,|y|\} is an element of \partial(J\times J), and that f_t(x,y)|_{\partial(J\times J)}=(x,y) due to the fact that \max\{|x|,|y|\}=1 on \partial(J\times J). Finally, note that continuity of the family f_t is given due to the fact that f_t is the composition of continuous functions of x,y,t for all t\in I. \,\,\square

2. Construct an explicit deformation retraction of \mathbb{R}^n\setminus\{0\} onto S^{n-1}.
Proof. This problem is essentially a problem from Calculus III. Note that for a vector \mathbf{x} in \mathbb{R}^n\setminus\{0\}, the normalized vector \mathbf{x}/\|\mathbf{x}\| lies on S^{n-1}. It suffices, then, to do the normalization process in a way that’s continuous for a time parameter t\in I, and one way to accomplish this is to define a family f_t:\mathbb{R}^n\setminus\{0\}\to S^{n-1} so that, for each \mathbf{x}=(x_1,x_2,\ldots,x_n) in the domain,

f_t(x_1,x_2,\ldots,x_n)=\left(\dfrac{x_1}{t\|\mathbf{x}\|+(1-t)},\cdots,\dfrac{x_n}{t\|\mathbf{x}\|+(1-t)}\right).

As noted in problem 1, the function f_t is continuous for each t\in I. Moreover, f_0(\mathbf{x})=\mathbf{x}, f_1(\mathbf{x})=\mathbf{x}/\|\mathbf{x}\|, and f_t(\mathbf{x})|_{S^{n-1}}=\mathbf{x} due to the fact that \|\mathbf{x}\|=1 for all \mathbf{x}\in S^{n-1}. \,\,\square

Catching Up

Posted by

0

So I managed to go nine months without ever looking at this thing. That’s unfortunate. It is, however, an indication of how the past two semesters have been for me, time-wise.

Without moving backwards, I’ll leave this for an update:

  • My GPA is pretty not-terrible.
  • I managed to exempt all of my qualifying exams by scoring A- or higher in the classes needed.
  • I’ve gotten to know some professors who seem not to hate me.
  • I’ve become a better mathematician.

All of those are important, of course, but the last one is the one that matters most.

When I started this thing, I’d meant it to be a place for sharing lots of general math stuff. Now that I (hopefully) have more time, I’m expecting more sharing to happen. Just to get things off on the right foot, here’s part of a little something I worked on last semester.

Here, we’re considering functions f:\mathbb{H}\to\mathbb{H} which are quaternion-valued functions of a quaternion variable. The function f is said to be (Feuter) Regular at q\in\mathbb{H} provided \overline{\partial}_\ell f(q)=0, where

\overline{\partial}_\ell=\dfrac{\partial}{\partial t}+i\dfrac{\partial}{\partial x}+j\dfrac{\partial}{\partial y}+k\dfrac{\partial}{\partial z}

The Cauchy-Fueter Integral Formula
If f is regular at every point of the positively-oriented parallelepiped K and q_0 is a point in the interior K^\circ of K, then

f(q_0)=\dfrac{1}{2\pi^2}\displaystyle\int_{\partial K} \dfrac{(q-q_0)^{-1}} {|q-q_0|^2} \,Dq\,f(q).

Proof. The proof given largely follows the outline given by Sudbury. For an equivalent statement translated from the language of differential forms into the framework of vector fields and their integrals, see the proof on page 12 of Deavours.

First, let K be a 4-parallelepiped in \mathbb{H} and let q_0 be an element of its interior K^\circ. Define the function g so that

g(q)=-\partial_r\left(\dfrac{1}{|q-q_0|^2}\right)=\dfrac{(q-q_0)^{-1}}{|q-q_0|^2},

where

\partial_r=\dfrac{\partial}{\partial t}-\dfrac{\partial}{\partial x}i-\dfrac{\partial}{\partial y}j-\dfrac{\partial}{\partial z}k.

Clearly, then, g is real differentiable at every point q\neq q_0 in K. Moreover, a simple computation verifies that \overline{\partial}_r g=0 except at q=q_0. From other results (see Sudbury), it follows that d(g\,Dq\,f)=0 for all q_0\neq q\in K^\circ by regularity of f.

Next, we use the dissection method from Goursat’s theorem. In particular, consider replacing K by a smaller parallelepiped \hat{K} for which q_0\in\hat{K}^\circ\subset K. Because f has a removable singularity at q=q_0, it follows that f is continuous at q_0, whereby it follows that choosing \hat{K} small enough allows approximation of f(q) by f(q_0). Finally, let S be a 3-sphere with center q_0 and Euclidean volume element dS on which

Dq=\dfrac{(q-q_0)}{|q-q_0|}dS.

Such substitution is possible by way of a change of variables in the definition of Dq. This change of variables results in the following:

\begin{array}{rcl} \displaystyle\int_{\partial K}\dfrac{(q-q_0)^{-1}}{|q-q_0|^2}Dq\,f(q) & = & \displaystyle\int_{\partial K}g\,Dq\,f(q) \\[1.5em] & = & \displaystyle\int_S g\,\dfrac{(q-q_0)}{|q-q_0|}dSf(q_0) \\[1.5em] & = &f(q_0)\displaystyle\int_S\dfrac{dS}{|q-q_0|^3}\\[1.5em] & = & f(q_0)\left(2\pi^2\right)\end{array}

Dividing both sides by 2\pi^2 yields the exact statement of the result. \,\square

The above is part of a (rather long) paper I finished last semester that’s in the infancy of a future as a potential pre-print/publication. I’m not going to link to it until I’ve done a bit more with it. Worth noting, too, is that this is the first time I’ve ever used WordPress’s incarnation of LaTeX, meaning there are many kinks to work out and much tinkering to do. I’m hoping that I can fit this blog into my plans for the rest of the semester, though, so maybe that will force me to do more with it.