So I managed to go nine months without ever looking at this thing. That’s unfortunate. It is, however, an indication of how the past two semesters have been for me, time-wise.
Without moving backwards, I’ll leave this for an update:
- My GPA is pretty not-terrible.
- I managed to exempt all of my qualifying exams by scoring A- or higher in the classes needed.
- I’ve gotten to know some professors who seem not to hate me.
- I’ve become a better mathematician.
All of those are important, of course, but the last one is the one that matters most.
When I started this thing, I’d meant it to be a place for sharing lots of general math stuff. Now that I (hopefully) have more time, I’m expecting more sharing to happen. Just to get things off on the right foot, here’s part of a little something I worked on last semester.
Here, we’re considering functions  which are quaternion-valued functions of a quaternion variable. The function
which are quaternion-valued functions of a quaternion variable. The function 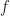 is said to be (Feuter) Regular at
is said to be (Feuter) Regular at  provided
provided  , where
, where

The Cauchy-Fueter Integral Formula
If 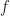 is regular at every point of the positively-oriented parallelepiped
is regular at every point of the positively-oriented parallelepiped 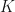 and
and 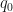 is a point in the interior
is a point in the interior  of
of 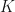 , then
, then

Proof. The proof given largely follows the outline given by Sudbury. For an equivalent statement translated from the language of differential forms into the framework of vector fields and their integrals, see the proof on page 12 of Deavours.
First, let 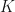 be a 4-parallelepiped in
be a 4-parallelepiped in 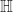 and let
and let 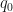 be an element of its interior
be an element of its interior  . Define the function
. Define the function  so that
so that

where

Clearly, then,  is real differentiable at every point
is real differentiable at every point  in
in 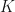 . Moreover, a simple computation verifies that
. Moreover, a simple computation verifies that  except at
except at  . From other results (see Sudbury), it follows that
. From other results (see Sudbury), it follows that  for all
for all  by regularity of
by regularity of 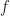 .
.
Next, we use the dissection method from Goursat’s theorem. In particular, consider replacing 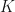 by a smaller parallelepiped
by a smaller parallelepiped  for which
for which  . Because
. Because 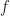 has a removable singularity at
has a removable singularity at  , it follows that
, it follows that 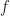 is continuous at
is continuous at 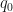 , whereby it follows that choosing
, whereby it follows that choosing  small enough allows approximation of
small enough allows approximation of  by
by  . Finally, let
. Finally, let 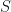 be a 3-sphere with center
be a 3-sphere with center 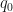 and Euclidean volume element
and Euclidean volume element  on which
on which

Such substitution is possible by way of a change of variables in the definition of  . This change of variables results in the following:
. This change of variables results in the following:
![\begin{array}{rcl} \displaystyle\int_{\partial K}\dfrac{(q-q_0)^{-1}}{|q-q_0|^2}Dq\,f(q) & = & \displaystyle\int_{\partial K}g\,Dq\,f(q) \\[1.5em] & = & \displaystyle\int_S g\,\dfrac{(q-q_0)}{|q-q_0|}dSf(q_0) \\[1.5em] & = &f(q_0)\displaystyle\int_S\dfrac{dS}{|q-q_0|^3}\\[1.5em] & = & f(q_0)\left(2\pi^2\right)\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D+%5Cdisplaystyle%5Cint_%7B%5Cpartial+K%7D%5Cdfrac%7B%28q-q_0%29%5E%7B-1%7D%7D%7B%7Cq-q_0%7C%5E2%7DDq%5C%2Cf%28q%29+%26+%3D+%26+%5Cdisplaystyle%5Cint_%7B%5Cpartial+K%7Dg%5C%2CDq%5C%2Cf%28q%29+%5C%5C%5B1.5em%5D+%26+%3D+%26+%5Cdisplaystyle%5Cint_S+g%5C%2C%5Cdfrac%7B%28q-q_0%29%7D%7B%7Cq-q_0%7C%7DdSf%28q_0%29+%5C%5C%5B1.5em%5D+%26+%3D+%26f%28q_0%29%5Cdisplaystyle%5Cint_S%5Cdfrac%7BdS%7D%7B%7Cq-q_0%7C%5E3%7D%5C%5C%5B1.5em%5D+%26+%3D+%26+f%28q_0%29%5Cleft%282%5Cpi%5E2%5Cright%29%5Cend%7Barray%7D&bg=ffffff&fg=111111&s=0&c=20201002)
Dividing both sides by  yields the exact statement of the result.
yields the exact statement of the result. 
The above is part of a (rather long) paper I finished last semester that’s in the infancy of a future as a potential pre-print/publication. I’m not going to link to it until I’ve done a bit more with it. Worth noting, too, is that this is the first time I’ve ever used WordPress’s incarnation of LaTeX, meaning there are many kinks to work out and much tinkering to do. I’m hoping that I can fit this blog into my plans for the rest of the semester, though, so maybe that will force me to do more with it.
