The Half-Week That Never Was

As I type this, it’s 2:45am on a Wednesday. I haven’t been around these parts since Sunday night (actually, 3:30am Monday morning), so one would think I’d have accumulated a ginormous list of professional doings to post proudly about here.

I regret to inform: That is not the case.

Movin’ on up (and down) (and up) (and down)….

I decided to spend as much time as possible today studying after a few days of being nonchalant with it. I went to bed early-ish last night, woke up early-ish this morning, and hit the books with very few breaks in between.

As it turns out, this recipe gave me ample opportunity to learn new things. Who woulda thunk?

I started with my professor’s paper on -conformal Cliffordian mappings. I made it through a couple more pages of that guy, verifying theorems and assertions as I went along. Then, right as I was on the precipice of real math, I realized how mentally taxing my morning had been and shifted direction a bit.

My new direction: Dummit and Foote. I started section 15.2 on Radicals and Affine Varieties. About 2/3 of the way through that section, I realized I really really need to learn some stuff about Gröbner Bases, so I decided to forego that and keep the ball rolling. I spent a few minutes flipping through Osborne’s book on Homological Algebra and upon realizing I’m far too underwhelming to tackle that guy, I shifted focus again to Kobayashi and Nomizu.

Of course, K&N has kind of worn out its welcome around here, and upon reading a page or two, I decided to break out a different Differential Stuff book instead. My target? Warner’s book Foundations of Differentiable Manifolds and Lie Groups. This book is a nice amalgam of Geometry and Topology, as evidenced by its somewhat nonstandard definition of tangent vectors. Maybe I’ll share some of that later.

Finally, I decided to shift my focus back towards Algebraic Geometry, whereby I broke out Eisenbud and Harris’s book The Geometry of Schemes and tried to stay afloat. Much to my own surprise, I was able to make it through fifteen-or-so pages without floundering completely and/or ripping all my hair out, so I’m hoping that maybe the information I’ve picked up in other places has done me some good. We’ll see for sure moving on.

Overall, I think I cranked out about 45-50 pages of reading today – and all (well, most) on material that’s completely new. It ain’t a Fields Medal, but it ain’t a flop either.

Until next time….

Working leisurely or Doing nothing?

So here’s the thing: I haven’t really done anything today. What I mean is that I haven’t constructed anything new (a page, a list of definitions, a solution) that didn’t exist yesterday, and so – for all intents and purposes – I haven’t done anything.

But somehow, I haven’t done nothing either.

Some days, I make a plan to do something (“do” something), and I set out on that path. Sometimes, the path I reach has a bunch of hurdles that I’m not prepared to conquer, and so I set out on a side journey to obtain the skills necessary to progress down my original path. Sometimes – on days that are particularly unkind – the side paths have hurdles requiring sidepaths and the side-side-paths have hurdles requiring side-side-paths and so the whole journey gets twisted into some amalgamated blob of non-progress that somehow still manages to accomplish something.

That, ladies and gentlemen, was a metaphor. It’s a metaphor that fits my day rather well.

So as I mentioned earlier, algebraic topology was a bust. I decided, then, to finally take the plunge and to read something on 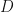-modules via Google. My professor had suggested this as a nice algebraic way to derive lots of the differential geometry results by way of learning really difficult algebra stuff like categories and stacks and sheaves and schemes and what not. That, of course, got me interested. I did a little digging and found an online resource from Harvard and decided to take a stab. I made it through about a page before I realized I was missing stuff on stuff.

I freshened up on stuff about Lie groups and took a gander at what Wikipedia had to say about Universal Enveloping Algebras. Of course, Universal Enveloping Algebras required me to know things about Tensor Algebras, and when I decided to look up something more foundational like “rings of differential operators”, I decided that I should probably concurrently try to parse through some literature regarding Differential Algebra as well. That chase has brought me to where I am now and has sustained me for the better part of three hours.

In that three hours, I’ve found lots of good resources (including an online .pdf of Ritt’s text Differential Algebra) and have done quite a bit of reading, but if I were to die today and pass the totality of today’s efforts off to someone else, their inheritance would consist of precisely zero tangible work.

So yea: Not doing anything while not doing nothing is a thing and it’s called “research mathematics”. Such is life, I suppose.

I think I’m going to end today’s part of my quest on the differential algebra / 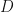-modules front here: I’ve got some stuff to do and what not, yadda yadda yadda, etc. etc. I plan on working some more on Kobayashi and Nomizu before bed, though.

All I do is math math math no matter what….